Answer:
A sample size of 551 is required.
Explanation:
We have that to find our
 level, that is the subtraction of 1 by the confidence interval divided by 2. So:
level, that is the subtraction of 1 by the confidence interval divided by 2. So:
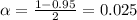
Now, we have to find z in the Ztable as such z has a pvalue of
 .
.
That is z with a pvalue of
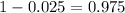 , so Z = 1.96.
, so Z = 1.96.
Now, find the margin of error M as such

In which
 is the standard deviation of the population and n is the size of the sample.
is the standard deviation of the population and n is the size of the sample.
Population standard deviation of 7 hours.
This means that
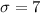
Determine the sample size required to have a margin of error of 0.585 hours.
This is n for which M = 0.585. So

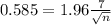
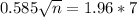

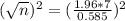
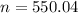
Rounding up(as for a sample of 550 the margir of error will be a bit above the desired target):
A sample size of 551 is required.