Question

NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. One hundred tickets, numbered 1, 2, 3, . . . , 100, are sold to 100 different people for a drawing. Four different prizes are awarded, including a grand prize (a trip to Tahiti). How many ways are there to award the prizes if it satisfies the given conditions. The person holding ticket 47 wins one of the prizes.

Answer 1

The total number of ways the person holding ticket 47 wins one of the prizes = 941,094

Explanation:

Given - One hundred tickets, numbered 1, 2, 3, . . . , 100, are sold to 100 different people for a drawing. Four different prizes are awarded, including a grand prize (a trip to Tahiti).

To find - How many ways are there to award the prizes if it satisfies the given conditions. The person holding ticket 47 wins one of the prizes.

Proof -

The order of selection is important because 1st selection is grand prize , 2nd selection is second prize and so on . So , we use permutation for this question

Now,

As The person holding ticket 47 wins one of the prizes and other 3 prizes are also given to the remaining 99 persons who got chosen

So,

The number of ways = 1* ⁹⁹P₃

=
`(99!)/((99-3)!)`

=
`(99!)/(96!)`

=
`(99*98*97*96!)/(96)`

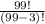
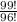
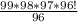
= 99*98*97

= 941,094

∴ we get

Total number of ways the person holding ticket 47 wins one of the prizes = 941,094