Answer:
a) The null hypothesis is
 and the alternate hypothesis is
and the alternate hypothesis is
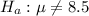
b) A test statistic of -2.06 should be used.
Step-by-step explanation:
Question a:
One water-treatment plant has a target pH of 8.5.
At the null hypothesis, we test if the mean is close to the target. So, the null hypothesis is:

At the alternate hypothesis, we test if it differs from 8.5, so the alternate hypothesis is:
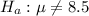
Question b:
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
8.5 is tested at the null hypothesis:
This means that

The mean and standard deviation of 1 hour's test results, based on 17 water samples at this plant, are 8.42 and 0.16, respectively.
This means that
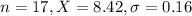
Value of the test statistic:

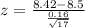
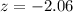
A test statistic of -2.06 should be used.