Question

Light with a wavelength of 600 nm shines onto a single slit, and the diffraction pattern is observed on a screen 2.5 m away from the slit. The distance, on the screen, between the dark spots to either side of the central maximum in the pattern is 25 mm. (a) What is the distance between the same dark spots when the screen is moved so it is only 1.5 m from the slit

Answer 1

"6.67 mm" is the right solution.

Step-by-step explanation:

The given values are:

• L = 2.5 m
• y = .0125
• λ = 600 nm

As we know, the equation

⇒
`(y)/(L) =(x \lambda)/(a)`

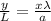
On substituting the values, we get

⇒
`(.0125)/(2.5)=((1)(600* 10^(-9)) )/(a)`

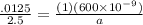
On applying cross multiplication, we get

⇒
`.0125a=2.5 (600* 10^(-9))`

⇒
`a=(2.5(600* 10^(-9)))/(.0125)`

⇒
`=1.2* 10^(-4) \ m`

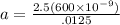
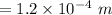
For new distance, we have to put this value of "a" in the above equation,

⇒
`(y)/(1.5) =((1)(600* 10^(-9)))/(1.2* 10^(-4))`

⇒
`(1.2* 10^(-4))y=1.5(600* 10^(-9))`

⇒
`y=(1.5(600* 10^(-9)))/(1.2* 10^(-4))`

⇒
`=3.22* 10^(-3) \ m`

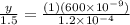
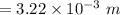
The total distance will be twice the value of "y", we get

=
`6.67* 10^(-3) \ m`

or,

=
`6.67 \ mm`