Question

1). What are the vertices of the hyperbola whose equation is:

( y + 6 ) ² ( x + 8 ) ²

_____ - _____

81 49


2). What are the foci of the hyperbola whose equation is:


( x - 6 ) ² ( y + 7 ) ²

_____ - _____

16 9

Answer 1

1) The vertices of the hyperbola are (-8, -15), (-8, 3)

2) The foci of the hyperbola are (11, -7) or (1, -7)

Explanation:

1) The vertices of a hyperbola given in the form
`(\left (y - k\right)^2)/(a^2) -(\left (x - h\right)^2)/(b^2) = 1` is (h, k ± a)

Therefore, for the given hyperbola with the following equation;

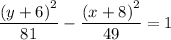`(\left (y + 6\right)^2)/(81) -(\left (x + 8\right)^2)/(49) = 1`, we have;

`(\left (y + 6\right)^2)/(9^2) -(\left (x + 8\right)^2)/(7^2) = 1`

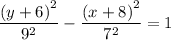
Therefore the vertices are;

(-8, -6 ± 9) = (-8, -15), (-8, 3)

2) The equation of the given hyperbola is presented as follows;

`(\left (x - 6\right)^2)/(16) -(\left (y + 7\right)^2)/(9) = 1`

The given hyperbola is of the form;

`(\left (x - h\right)^2)/(a^2) -(\left (y - k\right)^2)/(b^2) = 1`

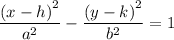
We get;

`(\left (x - 6\right)^2)/(4^2) -(\left (y + 7\right)^2)/(3^2) = 1`

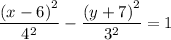
The foci is then (h ± c, k)

Therefore, by comparison, the foci of the given hyperbola is (6 ± c, -7)

Where c² = a² + b²

∴ c² = 4² + 3² = 25

c = √25 = 5

∴ The foci; (6 ± 5, -7) = (11, -7) or (1, -7).