Question

(a) A non-cold-worked 1040 steel cylindrical rod has an initial length of 100 mm and initial diameter of 7.50 mm. is to be deformed using a tensile load of 18,000 N. It must not experience either plastic deformation or a diameter reduction of more than 1.5 x 10-2 mm. Would the 1040 steel be a possible candidate for this application? Justify your choice(s) using calculations. For the 1040steel: Elastic modulus is 205 GPa, Yield strength is 450 MPa, and Poisson’s ratio is 0.27. (b) If you are asked to perform a strain hardening process to increase the yield strength so the steel can be used in another application with larger force load. How much cold work would be required to reduce the diameter of the steel to 6.0 mm?

Answer 1

A) 1040 steel is not a possible candidate for this application

B) 35.94%

Step-by-step explanation:

Initial length = 100 mm = 0.1 m

Initial diameter ( d ) = 7.5 mm = 0.0075 m

Tensile load ( p ) = 18,000 N

Condition : The 1040 steel must not experience plastic deformation or a diameter reduction of more than 1.5 * 10^-5 m

A) would the 1040 steel be a possible candidate for this application

Yield strength of 1040 steel < stress ( in order to be a possible candidate )

stress = p / A0 = ( 18000 ) / (
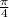`(\pi )/(4)` ) * 0.0075^2

= 18,000 / (4.418 * 10^-5 ) = 407.424 MPa

Yield strength of 1040 steel = 450 MPa

stress = 407.424 MPa

∴ Yield strength ( 450 MPa ) > stress ( 407.424 MPa )

Therefore 1040 steel is not a possible candidate for this application

B) Determine How much cold work would be required to reduce the diameter of the steel to 6.0 mm

Area1 = (
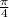`(\pi )/(4)` ) ( 0.006 )^2 = 2.83 * 10^-5 m^2

therefore % of cold work done = ( A0 - A1 ) / A0 * 100 = 35.94%