Answer:
(a) Expanded form:
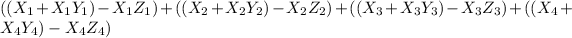
(b) The value of the expression: -21
Explanation:
Given
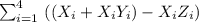
Solving (a): The expanded form:
This means that we substitute the values of i from 1 to 4 in the above expression.
So, the expression becomes:
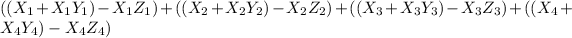
Solving (b): The value of the expression
To do this, we simply substitute the given values of X1, X2....... in the expression.
This gives:
So, the expression becomes:
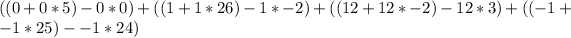
Simplify each bracket
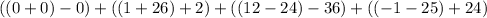
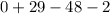
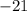
Hence, the result of the expression is -21