Answer:
The required confidence inteval = 94.9%.
Explanation:
Confidence interval: Mean ± Margin of error
Given: A confidence interval for the true mean diameter of all oak trees in the neighbourhood is calculated to be (36.191, 42.969).
i.e. Mean + Margin of error = 42.969 (i)
Mean - Margin of error = 36.191 (ii)
Adding (i) and (ii), we get
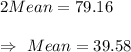
Margin of error = 42.969-39.58 [from (i)]
= 3.389
Margin of error =
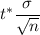
here n= 25
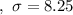
i.e.
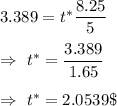
Using excel function 1-TDIST.2T(2.054,24)
The required confidence inteval = 94.9%.