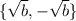19. A quadratic equation is shown below. a2-b=0 If b is a perfect square, which represents the solutions to the equation? HELP PLEASE

Question

asked Apr 5, 2022 126k views

1 Answer

Snapfla · Answer 1 · 2022-04-11T19:37:36+0000

Answer:

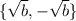
$\{\sqrt b, -\sqrt b\}$

Explanation:

Given

a^2 - b = 0

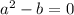
Required

Determine the solution

Since b is a perfect square, the equation can be expressed as:

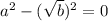
$a^2 - (\sqrt b)^2 = 0$

Apply difference of two squares:

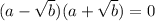
$(a - \sqrt b)(a + \sqrt b) = 0$

Split:

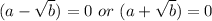
$(a - \sqrt b)= 0 \ or\ (a + \sqrt b) = 0$

Remove brackets:

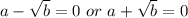
$a - \sqrt b= 0 \ or\ a + \sqrt b = 0$

Make a the subject in both equations

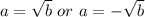
$a =\sqrt b \ or\ a =-\sqrt b$

The solution can be represented as:

$\{\sqrt b, -\sqrt b\}$