Question

Pierre was plotting the quadratic function f(x) = - x ^ 2 + 8x for an exit ticket His work is shown below .

Answer 1

(a) The table

`\begin{array}{cc}x & {f(x)} & {0} & {0} & {1} & {7}& {2} & {12} & {3} & {15} & {4} & {16} & {5} &{15} & {6} & {12} & {7} &{7} & {8} & {0}\ \end{array}`

(b) See attachment for graph

(c) He swapped the values of the x and y coordinates for one another

Explanation:

Given

See attachment for complete question

Solving (a): Complete the table

`f(x) = -x^2 + 8x`

`x = 0`:
`f(0) = -0^2 + 8*0 = 0 + 0 = 0`

`x = 1`:
`f(1) = -1^2 + 8*1 = -1 + 9 = 7`

`x = 2`:
`f(2) = -2^2 + 8 *2 = -4 + 16 = 12`

`x = 3`:
`f(3) = -3^2 + 8 *3 = -9 + 24 = 15`

`x = 4`:
`f(4) = -4^2 + 8 *4 = -16 + 32 = 16`

`x = 5`:
`f(5) = -5^2 + 8 *5 = -25 + 40 = 15`

`x = 6`:
`f(6) = -6^2 + 8 *6 = -36 + 48 = 12`

`x= 7`:
`f(7) = -7^2 + 8 *7 = -49 + 56 = 7`

`x = 8`:
`f(8) = -8^2 + 8 *8 = -64 + 64 = 0`

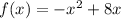
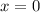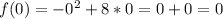
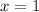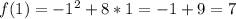
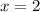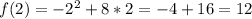
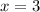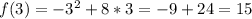
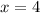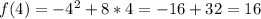
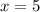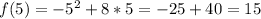
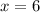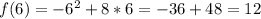
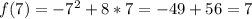
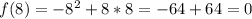
So, the complete table is:

`\begin{array}{cc}x & {f(x)} & {0} & {0} & {1} & {7}& {2} & {12} & {3} & {15} & {4} & {16} & {5} &{15} & {6} & {12} & {7} &{7} & {8} & {0}\ \end{array}`

Solving (b): Plot the graph

See attachment 2 for graph

Solving (c): Why he was marked as incorrect

By comparing the new attached graph (in b) and the graph of the original question, one will notice that the values of the x and y coordinates are switched.

This is why he was marked as incorrect.