Question

2. A marketing firm is trying to estimate the proportion of potential car buyers that would consider

purchasing a hybrid vehicle


a. The firm would like their pilot study to have a margin of error that is no more than 4%. How many


people should be in the pilot study in order to meet this goal at the 95% confidence level?


In a sample of 600 potential car buyers, 376 indicated that they would consider purchasing a hybrid


gas/electric powered car.


b. What is the point estimate for the proportion of potential car buyers that would consider buying a


hybrid vehicle? Calculate this value.


c. Find the 95% confidence interval for the true population proportion of potential car buyers that


would consider purchasing a hybrid vehicle.


d. Name two ways we could reduce the margin of error (Hint: think about the sample size n and the


confidence level)

Answer 1

a. The number of people that should be in the pilot study are 600 people

b. The point estimate is 0.62
`\overline 6`

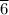
c. At 95% confidence level the true population proportion of potential car buyers of hybrid vehicle is between the confidence interval (0.588, 0.6654)

d. Two ways to reduce the margin of error are;

1) Reduce the confidence interval

2) Use a larger sample size

Explanation:

a. The given parameters for the estimation of sample size is given as follows;

The margin of error for the confidence interval, E = 4% = 0.04

The confidence level = 95%

The sample size formula for a proportion as obtained from an online source is given as follows;

`n = (Z^2 * P * (1 - P))/(E^2)`

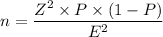
Where, P is the estimated proportions of the desired statistic, therefore, we have for a new study, P = 0.5;

Z = The level of confidence at 95% = 1.96

n + The sample size

Therefore, we have;

`n = (1.96^2 * 0.5 * (1 - 0.5))/(0.04^2) = 600.25`

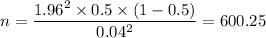
Therefore, the number of people that should be in the pilot study in order to meet this goal at 95% confidence level is n = 600 people

b. The point estimate for the population proportion is the sample proportion given as follows;

`\hat p = (x)/(n)`

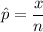
Where;

x = The number of the statistic in the sample

n = The sample size

From the question, we have;

The number of potential car buyers, n = 600

The number of respondent in the sample that indicated that they would consider purchasing a hybrid, x = 376

Therefore, the point estimate, for the proportion of potential car buyers that would consider buying a hybrid vehicle,
`\hat p` = 376/600 = 0.62
`\overline 6`

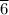
c. The confidence interval for a proportion is given as follows

`CI=\hat{p}\pm z* \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

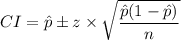
Therefore, we get;

`CI=0.62 \overline 6\pm 1.96* \sqrt{\frac{\hat{0.62 \overline 6}\cdot (1-\hat{0.62 \overline 6})}{600}}`

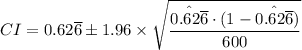
C.I. ≈ 0.6267 ± 0.0387

The 95% confidence interval for the true population proportion of potential buyers of hybrid vehicle, C.I. = (0.588, 0.6654)

d. The margin of error is given by the following formula;

`MOE_\gamma = z_\gamma * \sqrt{(\sigma ^2)/(n) }`

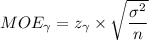
Where;

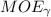`MOE_\gamma` = Margin of error at a given level of confidence

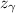`z_\gamma` = z-score

σ = The standard deviation

n = The sample size

Therefore, the margin error can be reduced by the following two ways;

1) Reducing the confidence interval and therefore, the z-score

2) Increasing the sample size