Question

You Try: Solve for x and y by using elimination. 4x + y = 7 4x - 2y = -2​

Answer 1

`\boxed {\boxed {\sf (1, 3) \ or \ x=1 \ and \ y=3}}}`

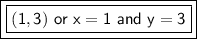
Explanation:

We are given this system of equations:

`4x+y=7\\4x-2y=-2`

We use elimination to solve to eliminate one of the variables, so we only have to work with one at a time. We do this by adding and subtracting the equations, and sometimes multiplying the entire equation by a number.

Notice how both equations have a 4x. This means they can easily be eliminated, without multiplying the equations by another number first. Let's subtract the 2 equations.

`\ \ \ 4x+y=7\\ -(4x-2y)=-2`

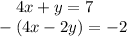
The 4x will cancel because 4x-4x=0.

`\ \ \ \ y=7 \\ - (-2y) = -2`

Since there are back to back negative signs, they become addition signs.

`\ \ \ \ y=7 \\+2y=2`

`3y=9`

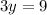
We are solving for y , so we must isolate the variable. It is being multiplied by 3 and the inverse of multiplication is division. Divide both sides by 3.

`3y/3=9/3\\y=3`

Now we can substitute 3 in for y in the original equations. Let's use the first one.

`4x+y=7\\4x+3=7`

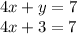
3 is being added to 4x. The inverse of addition is subtraction. Subtract 3 from both sides.

`4x+3-3=7-3\\4x=4\\`

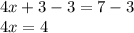
x is being multiplied by 4. The inverse of multiplication is division. Divide both sides by 4.

`4x/4=4/4\\x=1`

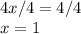
x is equal to 1 and y is equal to 3. Coordinate points are written as (x, y). The solution to this system of equations is (1, 3).