Answer:
the probability the person's reaction time will be between 0.9 and 1.1 seconds is 0.0378
Step-by-step explanation:
Given the data in the question;
the cumulative distribution function F(x) =
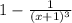 ;
;

probability the person's reaction time will be between 0.9 and 1.1 seconds
P( 0.9 < x < 1.1 ) = P( x ≤ 1.1 ) - P( x ≤ 0.9 )
P( 0.9 < x < 1.1 ) = F(1.1) - F(0.9)
= [
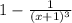 ] - [
] - [
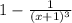 ]
]
we substitute
= [
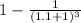 ] - [
] - [
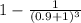 ]
]
= [
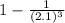 ] - [
] - [
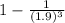 ]
]
= [
 ] - [
] - [
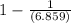 ]
]
= [ 1 - 0.1079796998 ] - [ 1 - 0.1457938 ]
= 0.8920203 - 0.8542062
= 0.0378
Therefore, the probability the person's reaction time will be between 0.9 and 1.1 seconds is 0.0378