Question

2. Carl needs 15 hours longer than Jennifer to paint a room. If they work together, they can complete the job in 4 hours. Explain each step in figuring out how to determine the time it would

take Jennifer to complete this job on her own. Pls help 20 minutes left

Answer 1

Jennifer would complete the job on her own in 5 hours.

Explanation:

Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

This polynomial has roots
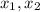`x_(1), x_(2)` such that
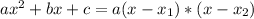`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\Delta))/(2*a)`

`x_(2) = (-b - √(\Delta))/(2*a)`

`\Delta = b^(2) - 4ac`

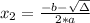
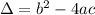
Rates

The together rate is the sum of their separates rate.

We have that:

Jennifer takes x hours to complete the job on her own, so her rate is 1/x.

Carl needs 15 hours longer than Jennifer, that is, 15 + x hours, so his rate is 1/(15+x).

The together rate is 1/4. So

`(1)/(4) = (1)/(x) + (1)/(15+x)`

`(1)/(4) = (15 + x + x)/(x(15+x))`

`(1)/(4) = (15 + 2x)/(x(15+x))`

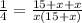
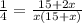
Applying cross multiplication.

`x^2 + 15x = 4(15 + 2x)`

`x^2 + 15x = 60 + 8x`

`x^2 + 7x - 60 = 0`

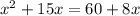
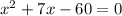
Quadratic equation with
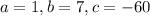`a = 1, b = 7, c = -60`. So

`\Delta = 7^(2) - 4*1*60 = 289`

`x_(1) = (-7 + √(289))/(2) = 5`

`x_(2) = (-7 - √(289))/(2) = -12`

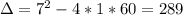
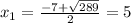
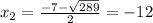
Since the time to complete the job has to be a positive value.

Jennifer would complete the job on her own in 5 hours.