Question

Know how to calculate point est., confidence interval, max tolerable error. Know the effect when you change the confidence level and the sample size. A high school surveyed their graduates on their starting salaries. 300 were returned. The average starting salary of the surveys returned was $32,000 with a standard deviation of $5,000.

1. What is the point estimate for the starting salary of the graduates?
2. What is the 95% confidence interval for the average salary of all graduates?
3. What is the value of the Maximum Tolerable Error for the above confidence interval?
4. If the level of confidence changes to 99%, and all other variables remain unchanged, what will happen to the confidence interval?
5. If the number of graduates returning the survey changes from 300 to 700, all other variables remaining unchanged, what will be effected?

Answer 1

1)The sample mean is the point estimate for the starting salary of the graduates which is $32,000

2) at 95%, confidence interval for the average salary of all graduates is ( 31525.13, 32474.87 )

3) Margin of Error E = 474.87

4) at 99%, confidence interval is ( 31328.54, 32671.46 ).

5) the probability of error will be affected

Explanation:

Given the data in the question;

1) the point estimate for the starting salary of the graduates?

The sample mean is the point estimate for the starting salary of the graduates which is $32,000

2) the 95% confidence interval for the average salary of all graduates?

given that;

mean x' = $32,000

standard deviation σ = $5000

sample size n = 300

∝ = 1 - 95% = 1 - 0.95 = 0.05

∝/2 = 0.05/2 = 0.025

Z Critical value
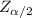`Z_{\alpha /2` = 1.6449 ≈ 1.645

so, 95% confidence interval for the average salary of all graduates will be;

⇒ x' ± Margin of Error

Margin of E =
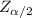`Z_{\alpha /2` ( σ/√n )

we substitute

E = 1.645( 5000/√300 )

E = 1.645( 288.675 )

E = 474.87

so

x' ± Margin of Error

32000 ± 474.87

⇒ 32,000 - 474.87, 32,000 + 474.87

⇒ ( 31525.13, 32474.87 )

Therefore, 95% confidence interval for the average salary of all graduates is ( 31525.13, 32474.87 )

3) the value of the Maximum Tolerable Error for the above confidence interval?

This is simply the Margin of Error,

Margin of Error E = 474.87

4)

If the level of confidence changes to 99%, and all other variables remain unchanged, what will happen to the confidence interval?

at 99% confidence level;

∝ = 1 - 99% = 1 - 0.99 = 0.01

∝/2 = 0.005

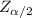`Z_{\alpha /2` = 2.326

∴ confidence interval will be;

⇒ 32000 ±
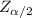`Z_{\alpha /2` ( σ/√n )

we substitute

⇒ 32000 ± 2.326( 5000/√300 )

⇒ 32000 ± 2.326( 288.675 )

⇒ 32000 ± 671.458

⇒ 32000 - 671.458, 32000 + 671.458

⇒ ( 31328.54, 32671.46 )

Therefore, at 99%, confidence interval is ( 31328.54, 32671.46 ).

5) If the number of graduates returning the survey changes from 300 to 700 and all other variables remaining unchanged, the probability of error will be affected