Question

A 97.3 kg horizontal circular platform rotates freely with no friction about its center at an initial angular velocity of 1.67 rad/s . A monkey drops a 9.67 kg bunch of bananas vertically onto the platform. They hit the platform at 45 of its radius from the center, adhere to it there, and continue to rotate with it. Then the monkey, with a mass of 21.9 kg , drops vertically to the edge of the platform, grasps it, and continues to rotate with the platform. Find the angular velocity of the platform with its load. Model the platform as a disk of radius 1.73 m

Answer 1

w = 1.14 rad / s

Step-by-step explanation:

This is an angular momentum exercise. Let's define a system formed by the three bodies, the platform, the bananas and the monkey, in such a way that the torques during the collision have been internal and the angular momentum is preserved.

Initial instant. The platform alone

L₀ = I w₀

Final moment. When the bananas are on the shelf

we approximate the bananas as a point load and the distance is indicated

x = 0.45m

L_f = (m x² + I ) w₁

angular momentum is conserved

L₀ = L_f

I w₀ = (m x² + I) w₁

w₁ =
`(I)/(m x^2 + I) \ w_o`

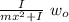
Let's repeat for the platform with the bananas and the monkey is the one that falls for x₂ = 1.73 m

initial instant. The platform and bananas alone

L₀ = I₁ w₁

I₁ = (m x² + I)

final instant. After the crash

L_f = I w

L_f = (I₁ + M x₂²) w

the moment is preserved

L₀ = L_f

(m x² + I) w₁ = ((m x² + I) + M x₂²) w

(m x² + I) w₁ = (I + m x² + M x₂²) w

we substitute

w =
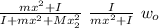
`(m x^2 +I)/(I + m x^2 + M x_2^2) \ (I)/(m x^2 + I) \ w_o`

w =
`(I)/(I + m x^2 + M x_2^2) \ w_o`

the moment of inertia of a circular disk is

I = ½ m_p x₂²

we substitute

w =
`( (1)/(2) m_p x_2^2 )/( (1)/(2) m_p x_2^2 + M x_2^2 + m x^2) \ \ w_o`

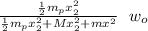
let's calculate

w =
`( (1)/(2) \ 97.3 \ 1.73^2 )/( (1)/(2) \ 97.3 \ 1.73^2 + 21.9 \ 1.73^2 + 9.67 \ 0.45^2 ) \ \ 1.67`

w =
`(145.60 )/(145.60 \ + 65.54 \ + 1.958) \ \ 1.67`

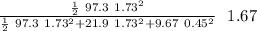
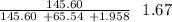
w = 1.14 rad / s