Answer:

Step-by-step explanation:
Given
Distance between two speakers is 8 m
Man is standing 12 away from the wall
When the person moves 3 parallel to the wall
the parallel distances from the speaker become 4+3, 4-3
Now, the difference of distances from the speaker is
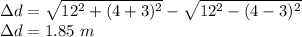
Condition for destructive interference is
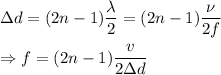
for second destructive interference; n=2
