Question

. A circular wire loop 40 cm in diameter has 100 Ohm resistance and lies in a horizontal plane. A uniform magnetic field points vertically downward, and in 25 ms it increases from 5 mT to 55 mT. Find the magnetic flux through the loop at (a) the beginning and (b) the end of 25 ms period. (c) What is the loop current during this time

Answer 1

(a) 6.283 Wb (b) 69.11 Wb (c) I = 0.628 A

Step-by-step explanation:

Given that,

The diameter of the loop, d = 40 cm

Radius, r = 20 cm

Initial magnetic field, B = 5 mT

Final magnetic field, B' = 55 mT

Initial magnetic flux,

`\phi_i=BA\\\\=5* 10^(-3)* \pi * 20^2\\\\=6.283\ Wb`

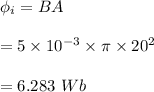
Final magnetic flux,

`\phi_f=B'A\\\\=55* 10^(-3)* \pi * 20^2\\\\=69.11\ Wb`

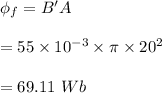
Due to change in magnetic field an emf will be generated in the loop. It is given by :

`\epsilon=-(d\phi)/(dt)\\\\=\phi_f-\phi_i\\\\=69.11-6.283\\\\=62.827\ V`

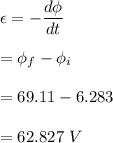
Let I be the current in the loop. We can find it using Ohm's law such that,

`\epsilon=IR\\\\I=(\epsilon)/(R)\\\\I=(62.827)/(100)\\\\=0.628\ A`

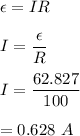
Hence, this is the required solution.