Answer:
at 99%, Confidence interval is ( 2.716, 3.285 )
( 2.716 < μ < 3.285 )
Explanation:
Given the data in the question;
sample size n = 8
mean x' = 3.0
standard deviation σ = 0.23
To calculate the confidence interval, we use the following expression;
x' ±
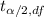 ( σ/√n) ------- let this be equation
( σ/√n) ------- let this be equation
now, at 99% confidence interval;
∝ = 1 - 99% = 1 - 0.99 = 0.01
degree of freedom df = n - 1 = 8 - 1 = 7
hence t-critical value = 3.499
in equation 1, we substitute in our values;
⇒ 3.0 ± 3.499( 0.23/√8 )
⇒ 3.0 ± 0.2845
⇒ 3.0 - 0.2845, 3.0 + 0.2845
⇒ ( 2.7155, 3.2845 )
Therefore at 99%, Confidence interval is ( 2.716, 3.285 )
( 2.716 < μ < 3.285 )