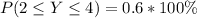Answer:
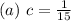
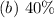
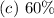
Explanation:
The given parameters can be represented as:
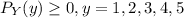
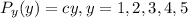
Solving (a): The value of c
To do this, we make use of the following rule;
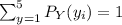
Given that:
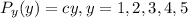
This is translated to:
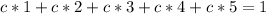
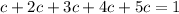

Solve for c
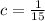
(b) The proportions of applications that requires at most 3 forms
This implies that: y = 1,2,3
So, we make use of:
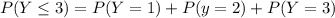
Recall that:
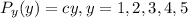
Substitute
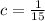
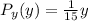
So:
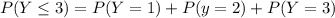

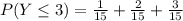
Take LCM
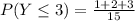

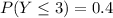
Express as percentage
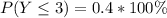
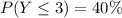
(c) The proportions of applications that requires between 2 and 4 forms (inclusive)
This implies that: y = 2,3,4
So, we make use of:
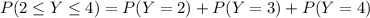
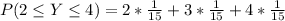
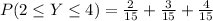
Take LCM
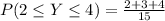
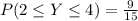
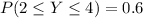
Express as percentage