Given:
The equation is:
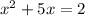
To find:
The solution of the given equation by completing the square.
Solution:
We have,
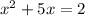
We need to add the square of half of the coefficient of x on both sides.
Adding
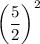 on both sides, we get
on both sides, we get
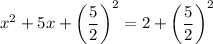
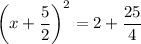
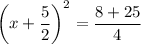
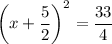
Taking square root on both sides, we get
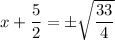
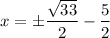
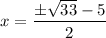
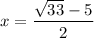 and
and
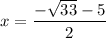
Therefore, the solutions of the given equation are
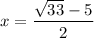 and
and
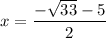 .
.