Answer:
Only 60 is an identified outlier
Explanation:
Given
Age group: 40 to 50
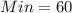
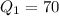
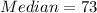
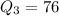
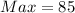
Conditions for outlier
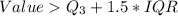
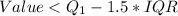
See attachment for complete question
Required
Which of 60, 62 and 84 is an outlier of age grout 40 to 50 years
First, calculate the IQR of group 40 to 50.
This is calculated as:
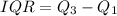
Where:
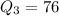 and
and
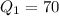
So:
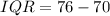
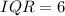
Next, is to test the outlier conditions on each value (i.e. 60, 62 and 84)
Testing 60
Condition 1
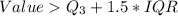
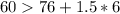
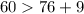
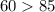 --- False
--- False
Condition 2
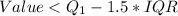


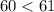 --- True
--- True
Because one of the conditions is true, then 60 is an outlier of group 40 - 50 years
Testing 62
Condition 1
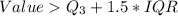
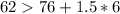
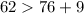
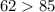 --- False
--- False
Condition 2
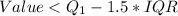


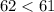 --- False
--- False
Because both conditions are false, then 62 is not an outlier of group 40 - 50 years
Testing 84
Condition 1
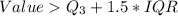
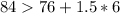
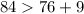
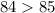 --- False
--- False
Condition 2
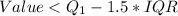


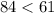 --- False
--- False
Because both conditions are false, then 84 is not an outlier of group 40 - 50 years