Answer:
a) The mean is 0.05 and the standard deviation is 0.0218.
b) v. The sampling distribution of p is not approximately normal because n(1 - p) is less than 10.
Explanation:
Central Limit Theorem
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
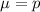 and standard deviation
and standard deviation
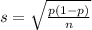 .
.
If
 and
and
 , the sampling distribution of the sample proportion p will be approximately normal.
, the sampling distribution of the sample proportion p will be approximately normal.
Consider the population consisting of all adult Americans age 65 and older who prefer to watch the news, and suppose that for this population the actual proportion who prefer to watch online is 0.05.
This means that
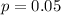
A random sample of n = 100 people
So
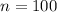
(a) What are the mean and standard deviation of the sampling distribution of p?
Mean
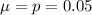
Standard deviation
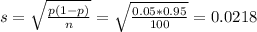
The mean is 0.05 and the standard deviation is 0.0218.
(b) Is the sampling distribution of p approximately normal for random samples of size n 100? Explain.
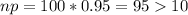
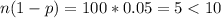
As n(1-p) < 10, it is not approximately normal, option v.