Question

Let the function P represent the population P(d), in thousands, of a colony of insect

d days after first being measured. A model for P is P(d) = 10. (1.08)". ​

Answer 1

(c) and (e) are true

Explanation:

Given

`P(d) = 10. (1.08)^d`

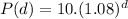
See attachment for complete question

Required

Which of the options is true

(a) 1080 insects on day 1

This implies that d = 1

So, we have:

`P(1) = 10* (1.08)^1`

`P(1) = 10* 1.08`

`P(1) = 10.8`

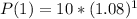
(a) is incorrect because
`P(1) \\e 1080`

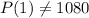
(b) 10800 insects after a week

This implies that
`d = 7`

So, we have:

`P(7) = 10* (1.08)^7`

`P(7) = 10* 1.71382426878`

`P(7) = 17.14`

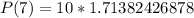
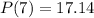
(b) is incorrect because
`P(7) \\e 10800`

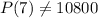
(c): Growth factor per day is 1.08

An exponential factor is represented as:

`y = ab^x`

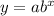
Where

b is the growth factor

By comparison:

`b = 1.08`

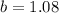
Hence, (c) option is true

(d): Growth factor per week is 1.08*7

In (c), we have:

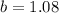`b = 1.08` as the daily growth factor

So, the growth factor for n days is:

`Factor = 1.08^n`

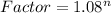
Substitute 7 for n i.e. 7 days

`Factor = 1.08^7`

So, the growth factor for 7 days is:
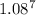`1.08^7` not
`1.08*7`

Hence, (d) option is true

(e): Growth factor per week is 1.08*7

In (c), we have:

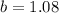`b = 1.08` as the daily growth factor

For hourly rate, we have:

`Factor = 1.08^(1)/(24)`

Hence, (e) option is true