Question

Consider a simple pendulum that consists of a massless 2.00-meter length of rope attached to a 5.00-kg mass at one end. What happens to the frequency of oscillation of the pendulum if we double the length of the rope

Answer 1

If we double the length we will have:

`f'=(f)/(√(2))`

Step-by-step explanation:

The equation of the angular frequency of a pendulum is given by:

`\omega=\sqrt{(g)/(L)}`

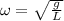
Where:

• g is the gravity
• L is the length of the pendulum

By definition the period is:

`T=(2\pi)/(\omega)`

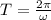
And frequency is 1 over the frequency T:

`f=(1)/(T)`

`f=(1)/(2\pi)\sqrt{(g)/(L)}`

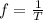
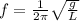
Now, if we double the length we will have:

`f'=(1)/(2\pi)\sqrt{(g)/(2L)}`

`f'=(1)/(2\pi√(2))\sqrt{(g)/(L)}`

`f'=(f)/(√(2))`

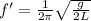
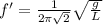
Therefore, the new frequency is the old frequency over √2.

I hope it helps you!