Question

Which line has the same slope as the lone passing through (-4,-1) and (-1,-7)

1) 6x+3y=5
2)y=-1/2x-7
3)y=-2

Answer 1

1) 6x+3y=5

Explanation:

1) First, find the slope of the line passing through (-4, -1) and (-1, -7). Use the slope formula
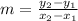`m = (y_2-y_1)/(x_2-x_1)`. Substitute the x and y values of the two points into the formula and solve:

`m = ((-7)-(-1))/((-1)-(-4)) \\m = (-7+1)/(-1+4) \\m = (-6)/(3) \\m = -2`

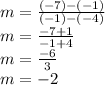
So, the slope is -2.

2) Now, identify the slopes of the lines in the options. We already know the slope of
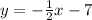`y = -(1)/(2) x-7` is
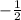`-(1)/(2)` since it is in slope-intercept form. y = -2 must have a slope of 0 since it's horizontal, and all equations with the format of y = a number are horizontal.

To find the slope of
`6x + 3y = 5`, isolate y to put the equations into slope-intercept form (
`y = mx + b` format), and whatever the coefficient of the x-term is will be the slope.

`6x + 3y = 5\\3y = -6x+5\\y = -2x + (5)/(3)`.

So, the slope of the first option is -2. It matches the slope we calculated in the first step, so that must be the answer.