This looks super complicated, but it can actually be solved with the application of a couple of area equations.
Let's establish one fact before we start this question that may have been the reason why this was so confusing for you. No matter what kind of triangle, the area will always be
 times the length of the base times height.
times the length of the base times height.
Alright, with that established, let's start trying to solve for the area.
In this question, we seem to have a triangle with a circle shape taken out of it. We are told to find the area of the shaded area.
The overall equation would be:
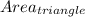 -
-
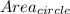
This makes sense, right? If we find the area of the triangle and subtract the area of the circle within it, it should give us the total shaded area.
Now, let's begin solving for said shaded area:
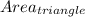 -
-
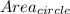
(
 * base * height) - (π*
* base * height) - (π*
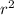 )
)
The given base of the triangle is 40 km, the height 27 km, and the circle's diameter is 12. Therefore:
(
 * 40 * 27) - (π *
* 40 * 27) - (π *
 )
)
(540) - (π *
 )
)
540 - 36π
Use 3.14 as the value for pi:
540 - 36(3.14)
426.96
Round to the nearest tenth:
427.0
Shaded area = 427 (
 )
)
If you have any questions on how I got to the answer, don't be afraid to ask!
- breezyツ