Question

According to the document Current Population Survey, published by the U.S. Census Bureau, 30.4% of U.S. adults 25 years old or older have a high school degree as their highest educational level. If 100 such adults are selected at random, determine the probability that the number who have ahigh school degree as their highest educational level is a. Exactly 32

Answer 1

0.0803 = 8.03% probability that the number who have a high school degree as their highest educational level is exactly 32.

Explanation:

For each adult, there are only two possible outcomes. Either they have a high school degree as their highest educational level, or they do not. The probability of an adult having it is independent of any other adult. This means that the binomial probability distribution is used to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

30.4% of U.S. adults 25 years old or older have a high school degree as their highest educational level.

This means that
`p = 0.304`

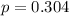
100 such adults

This means that
`n = 100`

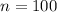
Determine the probability that the number who have a high school degree as their highest educational level is a. Exactly 32

This is P(X = 32).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 32) = C_(100,32).(0.304)^(32).(0.696)^(68) = 0.0803`

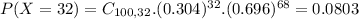
0.0803 = 8.03% probability that the number who have a high school degree as their highest educational level is exactly 32.