Question

1. Find all the values of x ∈ {0,2π) that satisfy the equation (sen(x)-cos(x))²=1+cos(x)

Answer 1

`\displaystyle x=\left\{(\pi)/(2), (7\pi)/(6), (3\pi)/(2), (11\pi)/(6)\right\}`

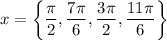
Explanation:

We are given the equation:

`(\sin(x)-\cos(x))^2=1+\cos(x)`

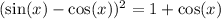
And we want to find all solutions for the equation within the interval [0, 2π).

First, we can expand. This yields:

`\sin^2(x)-2\sin(x)\cos(x)+\cos^2(x)=1+\cos(x)`

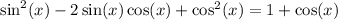
From the Pythagorean Identity, we know that:

`\sin^2(x)+\cos^2(x)=1`

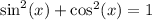
Therefore:

`-2\sin(x)\cos(x)+1=1+\cos(x)`

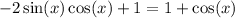
Simplify:

`-2\sin(x)\cos(x)=\cos(x)`

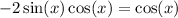
Subtract cos(x) from both sides*:

`-2\sin(x)\cos(x)-\cos(x)=0`

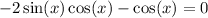
Factor:

`\cos(x)\left(-2\sin(x)-1)=0`

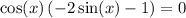
Zero Product Property:

`\cos(x)=0\text{ or } -2\sin(x)-1=0`

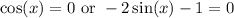
Solve for each case:

`\displaystyle \cos(x)=0\text{ or } \sin(x)=-(1)/(2)`

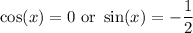
Use the unit circle. So, our solutions are:

`\displaystyle x=\left\{(\pi)/(2), (7\pi)/(6), (3\pi)/(2), (11\pi)/(6)\right\}`

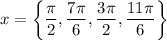
*Note that we should not simply divide both sides by cos(x) to acquire -2sin(x) = 1. This is because we do not know what the value of x is, and so one or may values of x may result in cos(x) = 0, and we cannot divide by 0. Hence, we need to subtract and factor and utilize the Zero Product Property.