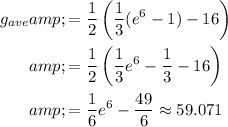Answer:
The average value of g is:
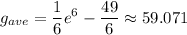
Explanation:
The average value of a function is given by the formula:
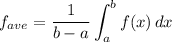
We want to find the average value of the function:
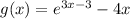
On the interval [1, 3].
So, the average value will be given by:
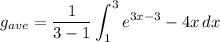
Simplify. We will also split the integral:
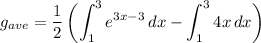
We can use u-substitution for the first integral. Letting u = 3x - 3, we acquire:
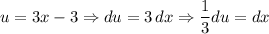
We will also change the limits of integration for our first integral. So:
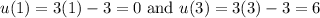
Thus:
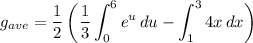
Integrate:
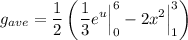
Evaluate. So, the average value of g on the interval [1, 3] is:
![\displaystyle g_(ave)=(1)/(2)\left((1)/(3)\left[e^6-e^0\right]-\left[2(3)^2-2(1)^2\right]\right)](https://img.qammunity.org/2022/formulas/mathematics/college/vt60rr8h2bzkoqgmrkzq33u2s27gx670zv.png)
Evaluate: