Answer:
The distance traveled by the tuning fork is 9.37 m
Step-by-step explanation:
Given;
source frequency,
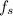 = 683 Hz
= 683 Hz
observed frequency,
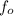 = 657 Hz
= 657 Hz
The speed at which the tuning fork fell is calculated by applying Doppler effect formula;
![f_o = f_s [(v)/(v + v_s) ]](https://img.qammunity.org/2022/formulas/physics/college/cx5s8qcde34gxevx21rfe6eu9awz4g43jb.png)
where;
 is speed of sound in air = 343 m/s
is speed of sound in air = 343 m/s
 is the speed of the falling tuning fork
is the speed of the falling tuning fork
![657 = 683[(343)/(343 + v_s) ]\\\\(657)/(683) = (343)/(343 + v_s)\\\\0.962 = (343)/(343 + v_s)\\\\0.962(343 + v_s) = 343\\\\343 + v_s = (343)/(0.962) \\\\343 + v_s = 356.55\\\\v_s = 356.55 - 343\\\\v_s = 13.55 \ m/s](https://img.qammunity.org/2022/formulas/physics/college/amojeuqpbqvyqwy139ojcu9ewm8d46j0m8.png)
The distance traveled by the tuning fork is calculated by applying kinematic equation as follows;
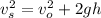
where;
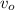 is the initial speed of the tuning fork = 0
is the initial speed of the tuning fork = 0
g is acceleration due to gravity = 9.80 m/s²
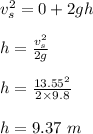
Therefore, the distance traveled by the tuning fork is 9.37 m