Answer: (0.00027144, 0.00036176)
Explanation:
The sample proportion of cell phone users who develop cancer of the brain or nervous system =
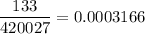
Sample size : 420027
Confidence interval for p:
 , where
, where
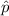 = sample proportion , n= sample size , z* = crirical z value.
= sample proportion , n= sample size , z* = crirical z value.
For 90% confidence interval , z*= 1.645
Required confidence interval:

A 90% confidence interval estimate of the percentage of cell phone users who develop cancer of the brain or nervous system = (0.00027144, 0.00036176)