Question

The function f(x) = -5x² + 20x + 55 models the height of a ball x seconds after it is thrown into the air. What is the total time that the ball is in the air?

Answer 1

The ball is in the air for about 5.873 seconds.

Explanation:

The function:

`f(x)=-5x^2+20x+55`

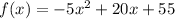
Models the height of a ball x seconds after it is thrown in the air.

And we want to find the total time the ball is in the air.

So, we can simply find the time x at which the ball lands. If it lands, its height f above the ground will be 0. Thus:

`0=-5x^2+20x+55`

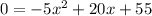
We will solve for x. Dividing both sides by -5 yields:

`0=x^2-4x-11`

The equation is unfactorable, so we can use the quadratic formula:

`\displaystyle x=(-b\pm√(b^2-4ac))/(2a)`

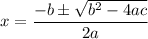
In this case, a = 1, b = -4, and c = -11. So:

`\displaystyle x=(-(-4)\pm√((-4)^2-4(1)(-11)))/(2(1))`

Evaluate:

`\displaystyle\begin{aligned} x&=(4\pm√(16+44))/(2)\\&=(4\pm√(60))/(2)\\&=(4\pm2√(15))/(2)\\&=2\pm√(15)\end{aligned}`

Approximate:

`x_1=2+√(15)\approx5.873\text{ or } x_2=2-√(15)\approx-1.873`

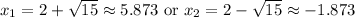
Since time cannot be negative, our only solution is the first choice.

So, the ball is in the air for about 5.873 seconds.