Answer:
The magnitude of the angular acceleration of the wheel is 14.53 rad/s².
Step-by-step explanation:
The angular acceleration can be found by using the following equation:
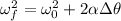 (1)
(1)
Where:
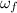 : is the final angular velocity = 18 rad/s
: is the final angular velocity = 18 rad/s
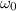 : is the initial angular velocity
: is the initial angular velocity
α: is the angular acceleration =?
Δθ = 19 rev*(2π/1 rev) = 119.4 rad
The initial angular velocity can be found knowing that the wheel turns through 19 revolutions during a 3 s time interval:
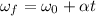
Where:
t: is the time = 3 s
By solving the above equation for ω₀ we have:
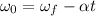 (2)
(2)
Now, by entering equation (2) into (1) we have:

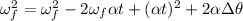
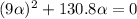
By solving the above equation for "α" we have:
α = -14.53
The minus sign means that the wheel is decelerating.
Hence, the angular acceleration of the wheel is -14.53 rad/s².
I hope it helps you!