Question

) If two half-open air columns A and B, that have identical lengths with one free and one fixed boundary, are subject to the same sound source frequency, what could explain why a wave may travel slower along column A compared to column B? Choose all that apply, and explain below. a) Column A has a slightly smaller diameter than column B. b) Column A is filled with argon gas, and column B is filled only with air. c) Column A and column B are identical in their fluid (i.e., air) density, except that the air in column A is at a higher temperature.

Answer 1

* for the condition the velocity in column A is less than in column B

all the answers are false

* the speed of sound in column A is greater than in column B

True b and c

Step-by-step explanation:

This interesting exercise we have a mixture of the resonance conditions and the conditions for the speed of sound.

The resonance condition is that at the closed end we have a node and at the open end a belly

λ = 4L first harmonic (fundamental)

The conditions of the speed of sound are

v =
`\sqrt{(B)/( \rho ) }`

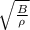
the velocity for air is v = 343 m/s at 20ºC and for argon it is v = 670 m/s at 20ºC

Another relationship is that the density of a gas depends on the temperature

v = v₀
`\sqrt{1 + (T)/(273) }`

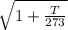
v₀ is the speed of sound at 0ºC

let's examine the different answers

* for the condition the velocity in column A is less than in column B

a) False. The resonance does not depend on the diameter but on the length of the column

b) False. The speed of sound in argon is greater than in air, the volume modulus of argon is greater

c) False. The speed depends on the root of the temperature, increasing the temperature increases the speed of sound.

As you can see in this case all the answers are false, let's change the condition

* the speed of sound in column A is greater than in column B

a) False

b) True

c) True