Question

Two in-phase sources of waves are separated by a distance of 3.50 m. These sources produce identical waves that have a wavelength of 5.96 m. On the line between them, there are two places at which the same type of interference occurs (a) Is it constructive or destructive interference, and (b) where are the places located?

Answer 1

(a) It is a destructive interference

(b) The places at which destructive interference occur on the line between the two in-phase sources, are 1.07798 m before and after the two sources

Step-by-step explanation:

(a) The given parameters are;

The distance between the two in-phase sources, d = 3.50 m

The type of waves produced by the two sources = identical waves

The wavelength of the waves produced by the two sources, λ = 5.96 m

For constructive interference, we have;

d·sin(θ) = m·λ

Where, m = 0, 1, -1, 2, -2, ...

For destructive interference, we have;

`d \cdot sin(\theta) = \left(m + (1)/(2) \right) \cdot \lambda`

d·sin(θ) = Δl =

Where, m = 0, 1, -1, 2, -2, ...

Therefore, given that λ > d, for constructive interference

sin(θ) = m·λ/d > 1 for m > 0 which is invalid as the maximum value for sin(θ) = 1

Therefore, the possible interference is destructive interference

(b) For destructive interference, when m = 0, we have;

`3.5 * sin(\theta) = \left(0 + (1)/(2) \right) * 5.96`

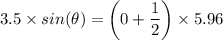
∴ sin(θ) = (5.96/2)/3.5

θ = arcsin((5.96/2)/3.5)

By trigonometry, we have;

tan(θ) = (d/2)/l

Where

l = The location along the line

∴ l = (d/2)/(tan(θ))

By substitution, we have;

l = (3.5/2)/(tan(arcsin((5.96/2)/3.5))) = 1.07798

Therefore, the two locations along the line where there is a destructive are 1.07798 m along the line before and after the two in-phase sources.