Question

Some types of bacteria contain chains of ferromagnetic particles parallel to their long axis. The chains act like small bar magnets that align these magnetotactic bacteria with the earth's magnetic field. In one experiment to study the response of such bacteria to magnetic fields, a solenoid is constructed with copper wire, 1.0 mmmm in diameter, evenly wound in a single layer to form a helical coil of length 40 cmcm and diameter 12 cmcm. The wire has a very thin layer of insulation, and the coil is wound so that adjacent turns are just touching. The solenoid, which generates a magnetic field, is in an enclosure that shields it from other magnetic fields. A sample of magnetotactic bacteria is placed inside the solenoid. The torque on an individual bacterium in the solenoid’s magnetic field is proportional to the magnitude of the magnetic field and to the sine of the angle between the long axis of the bacterium and the magnetic-field direction.

What current is needed in the wire so that the magnetic field experienced by the bacteria has a magnitude of 150μT?

a. 0.095 A
b. 0.12 A
c. 0.30 A
d. 14 A.

Answer 1

the required current is 0.12 A

Option b) 0.12 A is the correct answer

Step-by-step explanation:

Given the data in the question,

to determine the current needed in the wire, we use the following relation;

B = μ₀n
`I`

`I` = B / μ₀n

where μ₀ is the magnetic constant ( 4π × 10⁻⁷ T.m/A )

n is the number of turns ( 1 / 1mm
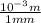`(10^(-3)m)/(1 mm)`) = 1000 m⁻¹

B is magnitude ( 150μT (
`(10^(-6)m)/(1uT)`) )

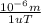so we substitute

`I` = [ 150μT (
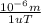`(10^(-6)m)/(1uT)`) ] / [ ( 4π × 10⁻⁷ T.m/A ) × 1000 m⁻¹ ]

`I` = [ 0.00015 ] / [ 0.00125 ]

`I` = 0.12 A

Therefore, the required current is 0.12 A

Option b) 0.12 A is the correct answer