Question

A small wooden block with mass 0.750 kg is suspended from the lower end of a light cord that is 1.40 m long. The block is initially at rest. A bullet with mass 0.0100 kg is fired at the block with a horizontal velocity v0. The bullet strikes the block and becomes embedded in it. After the collision the combined object swings on the end of the cord. When the block has risen a vertical height of 0.800 m, the tension in the cord is 5.00 N.

Required:
What was the initial speed v0 of the bullet?

Answer 1

The initial speed of the bullet will be:

`v_(ib)=331.36\: m/s`

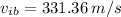
Step-by-step explanation:

Using the momentum conservation:

`p_(i)=p_(f)`

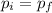
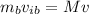`m_(b)v_(ib)=Mv` (1)

Where:

• M is the mass of the black plus the mass of the bullet
• v(ib) is the initial velocity of the bullet
• v is the velocity of the block with the bullet inside.

Using the conservation of energy:

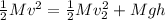`(1)/(2)Mv^(2)=(1)/(2)Mv_(2)^(2)+Mgh` (2)

Where v(2) is the speed of the system at 0.8 m of vertical height.

Using the forces acting on the system we can find v(2).

The forces can be equal to the centripetal force:

`T-Mg*sin(\alpha)=M(v_(2)^(2))/(L)`

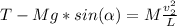
α is the angle of T with respect to the horizontal, here α = 25.4°

So, v(2) will be:

`T-Mg*sin(\alpha)=M(v_(2)^(2))/(L)`

`(L)/(M)(T-Mg*sin(\alpha))=v_(2)^(2)`

`(1.4)/(0.76)(5-0.76*9.81*sin(25.4))=v_(2)^(2)`

`v_(2)=1.82 \: m/s`

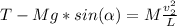
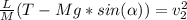
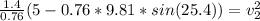
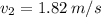
Using this value on equation (2) we will find v.

`v^(2)=v_(2)^(2)+2gh`

`v^(2)=1.82^(2)+2(9.81)(0.8)`

`v=4.36\: m/s`

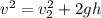
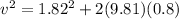
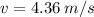
And finally using equation (1) we can find the initial speed of the bullet.

`m_(b)v_(ib)=Mv`

`0.01*v_(ib)=0.76*4.36`

`v_(ib)=331.36\: m/s`

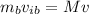
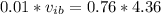
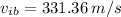
I hope it helps you!