Question

A cylinder has a radius of 4 inches and a height of 5 inches. If the radius of the cylinder is tripled and the height remains the same to create a new cylinder, what will be the difference in the surface areas of the two cylinders? Answer in terms of Pi.

Answer 1

Question:-

A cylinder has a radius of 4 inches and a height of 5 inches. If the radius of the cylinder is tripled and the height remains the same to create a new cylinder, what will be the difference in the surface areas of the two cylinders ? Answer in terms of Pi.

Answer:-

Given:-

A cylinder has a radius of 4 inches and a height of 5 inches.

To Find:-

If the radius of the cylinder is tripled and the height remains the same to create a new cylinder, what will be the difference in the surface areas of the two cylinders ?

Solution:-

Let in case of 1st cylinder,

`\bullet` Radius
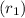`(r_1)` is 4 inches

`\bullet` Height is 5 inches

And in case of 2nd cylinder,

`\bullet` Radius
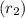`(r_2)` is 3 × 4 = 12 inches [as in the question it is given that the radius of the cylinder is tripled]

`\bullet` Height is 5 inches

Now,

Surface area
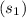`(s_1)` of 1st cylinder

is 2πr(r + h) = 2π × 4(4 + 5)

= 8π(9)

= 72π sq inches

Surface area
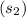`(s_2)` of 2nd cylinder

is 2πr(r + h) = 2π × 12(12 + 5)

= 24π(17)

= 408π sq inches

`\therefore` The difference in the surface areas of the two cylinders is =
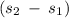`(s_2 \: - \: s_1)` = (408π - 72π) = 336π sq inches

The difference in the surface areas of the two cylinders is 336π sq inches. [Answer]

Answer 2

• 336π in²

Explanation:

Cylinder 1

• r₁= 4 in
• h = 5 in

Cylinder 2

• r₂ = 3*4 = 12 in
• h = 5 in

Surface area of cylinders:

• S = 2πr(r + h)

• S₁ = 2π*4*(4 + 5) = 72π in²
• S₂ = 2π*12*(12 + 5) = 408π in²

The difference is:

• S₂ - S₁ =
• 408π - 72π =
• 336π in²