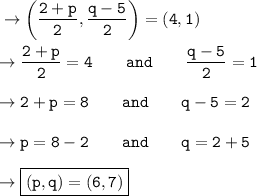Explanation:
Three coordinates of a Rhombus is given to us. And the fourth coordinate is D(p,q) . Weneedtofind the value of p and q . We know that the diagonals of Rhombus bisect each other at right angles . So lets find the midpoint.
• Midpoint of AC :-
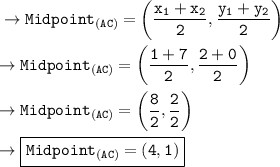
_______________________________
• Midpoint of BD :-
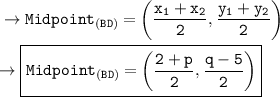
_______________________________
Now since these two coordinates must be equal, therefore ,