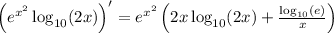Question

Help!!
differentiate

`{ {e}^(x) }^(2) log_(10)(2x)`
​

Answer 1

Rewrite the function using the change-of-base identity as

`e^(x^2) \log_(10)(2x) = e^(x^2) (\ln(2x))/(\ln(10))`

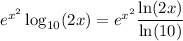
Apply the product rule:

`\left(e^(x^2) \log_(10)(2x)\right)' = \left(e^(x^2)\right)' (\ln(2x))/(\ln(10)) + e^(x^2) \left((\ln(2x))/(\ln(10))\right)'`

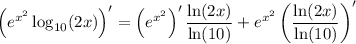
Use the chain rule:

`\left(e^(x^2) \log_(10)(2x)\right)' = e^(x^2)\left(x^2\right)' (\ln(2x))/(\ln(10)) + e^(x^2) ((2x)')/(2\ln(10)x)`

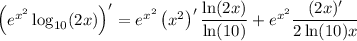
Compute the remaining derivatives:

`\left(e^(x^2) \log_(10)(2x)\right)' = 2xe^(x^2) (\ln(2x))/(\ln(10)) + e^(x^2) \frac2{2\ln(10)x} = e^(x^2)\left((2x\ln(2x))/(\ln(10)) + \frac1{\ln(10)x}\right)`

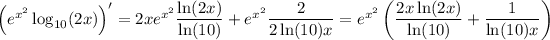
If you like, you can convert back to base-10 logarithms:

ln(2x) / ln(10) = log₁₀(2x)

1 / ln(10) = ln(e) / ln(10) = log₁₀(e)

Then

`\left(e^(x^2) \log_(10)(2x)\right)' = e^(x^2)\left(2x\log_(10)(2x)+\frac{\log_(10)(e)}x\right)`