Question

If S_1=1,S_2=8 and S_n=S_n-1+2S_n-2 whenever n≥2. Show that S_n=3⋅2n−1+2(−1)n for all n≥1.

Answer 1

You can try to show this by induction:

• According to the given closed form, we have
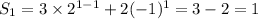`S_1=3*2^(1-1)+2(-1)^1=3-2=1`, which agrees with the initial value S₁ = 1.

• Assume the closed form is correct for all n up to n = k. In particular, we assume

`S_(k-1)=3*2^((k-1)-1)+2(-1)^(k-1)=3*2^(k-2)+2(-1)^(k-1)`

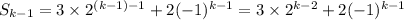
and

`S_k=3*2^(k-1)+2(-1)^k`

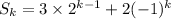
We want to then use this assumption to show the closed form is correct for n = k + 1, or

`S_(k+1)=3*2^((k+1)-1)+2(-1)^(k+1)=3*2^k+2(-1)^(k+1)`

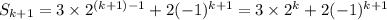
From the given recurrence, we know

`S_(k+1)=S_k+2S_(k-1)`

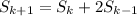
so that

`S_(k+1)=3*2^(k-1)+2(-1)^k + 2\left(3*2^(k-2)+2(-1)^(k-1)\right)`

`S_(k+1)=3*2^(k-1)+2(-1)^k + 3*2^(k-1)+4(-1)^(k-1)`

`S_(k+1)=2*3*2^(k-1)+(-1)^k\left(2+4(-1)^(-1)\right)`

`S_(k+1)=3*2^k-2(-1)^k`

`S_(k+1)=3*2^k+2(-1)(-1)^k`

`\boxed{S_(k+1)=3*2^k+2(-1)^(k+1)}`

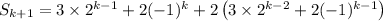
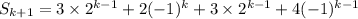
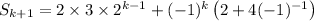
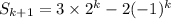
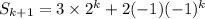
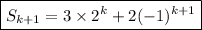
which is what we needed. QED