Answer:
-1.517
Need to know:
Integral constant rule: ∫ (ax)dx = a ∫ (x)dx
Integral power rule: ∫ xⁿ = xⁿ⁺¹/(n + 1)
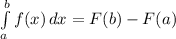
Quadratic formula:
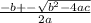
Explanation:
First, we have to find the average value of f over the interval [-2, 2]
To find that, calculate the integral of 3x(x - 2)
∫ 3x(x - 2)dx = 3 ∫ x(x - 2)dx = 3 ∫ x² - 2xdx (pulled out the 3 because of the constant rule)
Use the power rule to solve the integral
3 [x²⁺¹/(2 + 1) - 2x¹⁺¹/(1 + 1)] = 3[x³/3 - 2x²/2]
Distribute the 3
3[x³/3 - 2x²/2] = x³ - 3x² = F(x)
We plug in 2 in place of x
F(2) = 2³ - 3(2)² = -4
Do the same with -2
F(-2) = (-2)³ - 3(-2)² = -20
We have to remember that
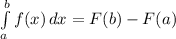
let a = -2 b = 2
F(2) - F(-2) = -4 - (-20) = -4 + 20 = 16
The average value of f over the given interval is 16.
Now we make it to where f(x) = 16 to find c
3x(x - 2) = 16
3x² - 6x = 16
Subtract 16 from both sides to make it equal to zero
3x² - 6x = 16
- 16 - 16
3x² - 6x - 16 = 0
a = 3 b = -6 c = 16
Plug these numbers into the quadratic formula
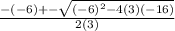
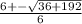
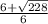 = -1.51661
= -1.51661
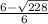 = 3.51661
= 3.51661
-1.51661 is the only number out of the two that fits in the given interval [-2,2], so c would have to be -1.517 in order for f(c) to equal the average value of f over the given interval.