All we really need to pull from the paragraph are the following details:
"John has a cylindrical container ... while Susie has a cone. John's container has a radius of 6 inches and a height of 10 inches while Susie's container has the same base and equal height."
a. Find the volume of each container.
[] We can solve this by solving for the volumes via known mathematical formulas
John's Cylindrical Container is about 1,130.97 inches cubed
-> V = πr²h
-> V = π6²10
-> V ≈ 1130.97
Susie's Cone is about 376.99 inches cubed
-> V = πr²
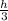
-> V = π6²
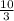
-> V ≈ 376.99
b. How many times will Susie need a refill in order to have the same amount of smoothie as John? Verify your reasoning.
[] Let x be the number of times Susie refills her cone.
1,130.97 = 376.99x
3 = x
x = 3
Suize will refill her cone 3 times
c. If John finds a container that is half the height of his previous container but has the same size base, how will the volume of John's new container compare to Susie's cone-shaped container?
[] We will assume that John still has a cylindrical container.
[] Using the same formula from step one, we will solve for the volume of the new contaier
[] 10 / 2 = 5, so the new height is 5 inches
-> V = πr²h
-> V = π6²5
-> V ≈ 565.49
[] Now we will compare this to Suise's container
-> 565.49 - 376.99 = 188.5 inches cubed
-> 565.49 / 376.99 ≈ 1.5
John's container will be about 1.5 times larger than Suise's, or 188.5 inches cubed larger.