Question

A disk of radius 25 cm spinning at a rate of 30 rpm slows to a stop over 3 seconds. What is the angular acceleration?

B. How many radians did the disk turn while stopping ?
C. how many revolutions?

​

Answer 1

A. α = - 1.047 rad/s²

B. θ = 14.1 rad

C. θ = 2.24 rev

Step-by-step explanation:

A.

We can use the first equation of motion to find the acceleration:

`\omega_f = \omega_i + \alpha t\\`

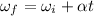
where,

ωf = final angular speed = 0 rad/s

ωi = initial angular speed = (30 rpm)(2π rad/1 rev)(1 min/60 s) = 3.14 rad/s

t = time = 3 s

α = angular acceleration = ?

Therefore,

`0\ rad/s = 3.14\ rad/s + \alpha (3\ s)\\`

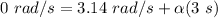
α = - 1.047 rad/s²

B.

We can use the second equation of motion to find the angular distance:

`\theta = \omega_i t + (1)/(2)\alpha t^2\\\theta = (3.14\ rad/s)(3\ s) + (1)/(2)(1.04\ rad/s^2)(3\ s)^2\\`

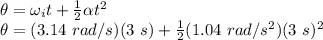
θ = 14.1 rad

C.

θ = (14.1 rad)(1 rev/2π rad)

θ = 2.24 rev