Answer:
The value of g(2.7) is 31.49.
Explanation:
Translations of a function:
Suppose that we have a function f(x).
The translation of f(x) a units to the left is given by g(x) = f(x+a).
The translation of f(x) a units to the right is given by g(x) = f(x-a).
The translation of f(x) a units up is given by g(x) = f(x) + a.
The translation of f(x) a units down is given by g(x) = f(x) - a.
Suppose the graph of f(x)=x^2 is translated 3 units right and 1 unit down.
Three units right:
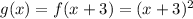
One unit down:

What is the value of g(2.7)?
This is g when
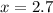 . So
. So
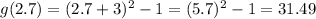
The value of g(2.7) is 31.49.