Find the common difference, d, given that 8x-3, 4x+1, 2x-2 are consecutive terms of an arithmetic sequence. A)1/6 B) -10 C) 10 D) 5

Question

asked Aug 20, 2022 113k views

2 Answers

Ufo · Answer 1 · 2022-08-24T13:09:47+0000

Answer:

B

Explanation:

We are given that:

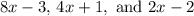
$8x-3, \, 4x+1, \text{ and } 2x-2$

Are consecutive terms of an arithmetic sequence.

And we want to determine the common difference d.

Recall that for an arithmetic sequence, each subsequent term is d more than the previous term.

In other words, the second term is one d more than the first term. So:

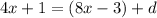
4x+1=(8x-3)+d

And the third term is two d more than the first term. So:

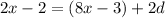
2x-2=(8x-3)+2d

We can isolate the d in the first equation:

-4x+4=d

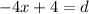
As well as the second:

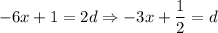
$-6x+1=2d\Rightarrow \displaystyle -3x+(1)/(2)=d$

Then by substitution:

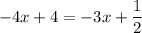
$\displaystyle -4x+4=-3x+(1)/(2)$

Solve for x:

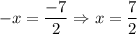
$\displaystyle -x=(-7)/(2)\Rightarrow x=(7)/(2)$

The isolated first equation tells us that:

d=-4x+4

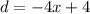
Therefore:

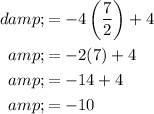
$\begin{aligned} \displaystyle d&=-4\left((7)/(2)\right)+4\\&=-2(7)+4\\&=-14+4\\&=-10 \end{aligned}$

Our final answer is B.