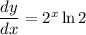Answer:
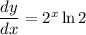
Explanation:
**This is a non-linear function and therefore does not have a constant rate of change. It will have a different slope depending on what points you use in the average rate of change formula:

To calculate rate of change, differentiate.
substitute y for
 :
:

Take natural logs of both sides:

Apply the log rule
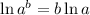 :
:
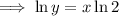
Differentiate with respect to
 :
:
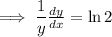
Mulitply both sides by
 :
:
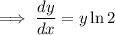
Replace
 with
with
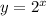
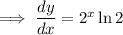
Therefore, rate of change of the function is :