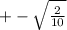Explanation:
We are given a theta degree measure of sin in a specific interval. We are asked to find half of that degree measure.
The interval it ask us to find it in is between 2 pi and 5 pi over 2.
That is 360 degrees to 450 degrees. If you use reference angles, that is between the 0 degrees and 90 degrees. So that means our measure is going to be in the 1st quadrant.
Replace x with theta
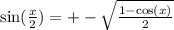
We dont know cos x but we can use the pythagorean trig theorem to find cos x.

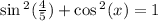
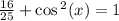



Cosine in 1st quadrant is positive so 3/5 is cos x.
Replace 3/5 for cos x.

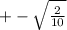
The answer is