Question

Amanda deposits $2,000 into a CD with 4% interest and is compounded monthly. How much

will be in the account after 4 years?

Answer 1

$2,346.40 (nearest cent)

Step-by-step explanation:

`B = P(1 + (r)/(n))^(nt)`

where B is the balance, P is the principal amount, r is the interest rate in decimal format, t is the time in years and n is the number of times interest is compounded per year

• P = 2000
• r = 4% = 4/100 = 0.04
• n = 12
• t = 4

`\implies B = 2000(1 + (0.04)/(12))^(4*12)`

`\implies B = \$2346.40`

Answer 2

there will be $2346.40 after 4 years.

Step-by-step explanation:

`\sf A = P(1 + (r)/(n) )^(nt)`

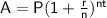
"A" - money after compound interest, "P" - money deposited, "r" - rate of interest, "t" - time (years)

given:

• P = $2000
• r = 4%
• t = 4 years

using the formula:

`\sf A = 2,000(1 + (0.04)/(12) )^(12*4)`

`\sf A = 2,346.40`

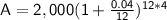
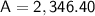
'compounded monthly so n will be 12 months'